Vad är Divisors of 30?
Du kan snabbt veta vilka divisorerna är av 30, liksom alla andra nummer (nonzero), men den grundläggande tanken är att lära sig hur divisorerna av ett tal beräknas på ett allmänt sätt.
Försiktighet bör vidtas när diskussionerna diskuteras, eftersom det snabbt kan fastställas att alla divisorer på 30 är 1, 2, 3, 5, 6, 10, 15 och 30, men hur är negativet av dessa nummer? ? Är de delare eller inte?
För att svara på den tidigare frågan är det nödvändigt att förstå en mycket viktig term i matematikens värld: divisionalgoritmen.
Divisionens algoritm
Divisionsalgoritmen (eller euklidiska divisionen) säger följande: Med två heltal "n" och "b", där "b" skiljer sig från noll (b ≠ 0) finns det bara heltal "q" och "r" så att n = bq + r, där 0 <r <| b |.
Numret «n» kallas en utdelning, «b» kallas en divisor, «q» kallas kvotient, och «r» kallas resten eller återstoden. När resten "r" är lika med 0, sägs att "b" delar "n", och detta betecknas med "b | n".
Divisionalgoritmen är inte begränsad till positiva värden. Därför kan ett negativt tal vara en divisor av ett annat nummer.
Varför är 7.5 inte en divisor på 30?
Med divisionsalgoritmen kan man se att 30 = 7, 5 × 4 + 0. Resten är lika med noll, men det kan inte sägas att 7, 5 delar upp till 30 eftersom, när man talar om divisorer, talar man enbart om heltal.
Dividers of 30
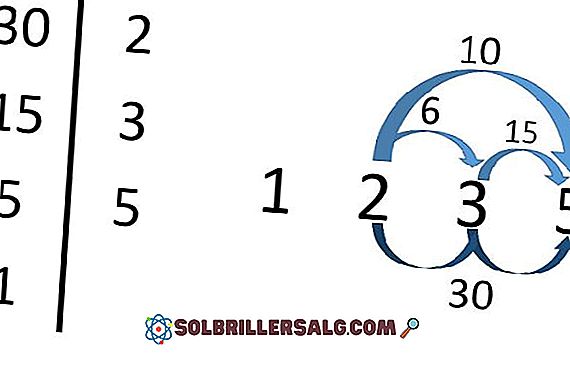
Som framgår av bilden, för att hitta divisorerna på 30 måste du först hitta sina primära faktorer.
Därefter 30 = 2x3x5. Av detta dras slutsatsen att 2, 3 och 5 är divisorer på 30. Men så är produkterna av dessa primära faktorer.
Så 2 × 3 = 6, 2 × 5 = 10, 3 × 5 = 15 och 2x3x5 = 30 är divisorer av 30. Den 1 är också en divisor på 30 (även om det faktiskt är en divisor av något nummer).
Man kan dra slutsatsen att 1, 2, 3, 5, 6, 10, 15 och 30 är divisorer på 30 (alla uppfyller divisionens algoritm), men vi måste komma ihåg att deras negativa är också divisorer.
Därför är alla divisorer av 30: -30, -15, -10, -6, -5, -3, -2, -1, 1, 2, 3, 5, 6, 10, 15 och 30 .
Vad som har lärt sig ovan kan appliceras med ett helt tal.
Om du till exempel vill beräkna divisorerna på 92 fortsätter du som tidigare. Den sönderdelas som en produkt av primtal.
Dela 92 med 2 och få 46; Nu 46 är uppdelad med 2 igen och du får 23.
Detta sista resultat är ett primtal, så det kommer inte att ha fler divisorer förutom 1 och samma 23.
Vi kan då skriva 92 = 2x2x23. Förlopp som tidigare dras slutsatsen att 1, 2, 4, 46 och 92 är divisorer av 92.
Slutligen inkluderar vi negativen av dessa nummer till föregående lista, så att listan över alla divisorerna på 92 är -92, -46, -4, -2, -1, 1, 2, 4, 46, 92.